1. Pandiagonal Squares

In 1998, I wrote a program in Turbo Pascal to calculate pandiagonal squares of order 7 (reduced program/2 352 and with 24 parameters). On a K6 computer running at 200 MHz, this program worked correctly (I had made many tests), but it didn't give solutions! I had solutions only if I fixed starting conditions in a domain where I knew there were solutions. In 2004, on a Duron running at 1.4 GHz, the same program translated in C was much more faster but still didn't give solutions.

I think there are too many cases to examine: the limits of existing personal computers are reached, even if my program isn't optimized.

Note # 1: I remember that the pandiagonal squares of order 7 haven't a group structure. The order of group G is probably 2 352, but I am not absolutely sure. See page The transformation method, § 4.3 and § 4.4. It is for me an open question.

Note # 2: a program with 23 imbricate loops works correctly for order 6 (see Appendix 5, § 1) when you search orthogonal squares to Latin diagonal squares. I think the reason is the number of cases to examine which is smaller.

2. Symmetrical Pandiagonal Squares

If the enumeration of pandiagonal squares is not possible today with personal computers, on the contrary the enumeration of symmetrical pandiagonal squares is possible (program with only 12 parameters).

• The number of symmetrical pandiagonal squares was first calculated by Walter TRUMP in 2001 with a reduced program/48 written in GB32, a German programming language (see Walter TRUMP's site).
  
  On this site, you will see that I found in June 2004 the same result in 12 days with a program in C running on a Duron 1.4 GHz and with a reduced program/96.
  
  It is sure that the order of group G is 96 because the number of elementary squares found with a reduced program/96 is a prime (cf. Walter TRUMP's site).
  
  I can explain how I found the new transformation W of order 2 that allowed me to have a reduced program/96 (the other 48 transformations of group G are transpositions).
  I found transformation W occasionally in August 2000, when trying to compute the number of semi-regular symmetrical pandiagonal squares.
  I had a reduced program/48 with A1 equal to the minimum of the 24 values in the 2 diagonals, fourth column and fourth row, and with A7< G1). I computed the numbers of solutions for different values of A1 and A2, specially at the border of domain (A1, A2) where the number of solutions is very low. I found 5 solutions for A1=8 and A2=49, and 3 solutions for A1=8 and A2=48. I examined these squares and found that the transformation W between the first square (A1=8, A2=49) and the first square (A1=8, A2=48) was very simple.
  These two squares are (I give only the first row for each one):

  8	49	4	27	31	39	17	and
  8	48	4	32	31	35	17.

  When writing the conditions of transformation W (in function of the 12 parameters), I found identities. Therefore, W was a transformation for any symmetrical pandiagonal square.
  
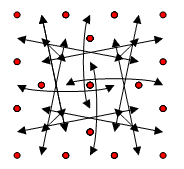
  I give the matrix of definition and the graph of W:
  
  

  A1 F3 A3 E4 A5 F5 A7 C6 C3 G2 B4 G6 C5 C2 C1 B7 B2 G4 B6 B1 C7 D5 D2 D7 D4 D1 D6 D3 E1 F7 F2 A4 F6 F1 E7 E6 E3 A2 F4 A6 E5 E2 G1 B3 G3 C4 G5 B5 G7

  
  I tried to identify the group of order 96 and the subgroup of order 48 among the well-known groups in the literature: I wasn't successful. I only found some abstract definition relations.
  
  Question: can anyone identify these groups?
  
  
• I calculated in August 2004 the number of semi-regular symmetrical pandiagonal squares. See page The intermediate square method, § 6.
  
  Note: for these squares, a group G' (permutations) of order 8 operates - besides the group G (transformations) of 96 - , the symmetry about the centre being common to the transformations. Finally, a semi-regular symmetrical pandiagonal square generates:
  96 * 4 = 384 squares generally,
  96 * 2 = 192 squares sometimes.
  
  The number of regular symmetrical squares can be easily calculated: 27 648 squares are found (576 elementary squares with the above group G of order 48; the transformation W is an external transformation to the set).
  
  
• Irregular symmetrical pandiagonal squares are the most numerous, regular or semi-regular squares are the exception.
  I remember that for irregular squares, the sum of capital letters is different from 147 with A=0, B=7, C=14,..., G=42.
  I searched irregular symmetrical pandiagonal squares with a maximum number of irregular lines (i. e. rows, columns or broken diagonals). I found in September 1998 two examples of symmetrical pandiagonal squares with 24 irregular lines (24 is the maximum for a symmetrical pandiagonal square, because the 2 diagonals, the 4^th row and the 4^th column can't be irregular):
  
  

  1 47 27 29 39 15 17 44 12 13 28 4 48 26 19 32 14 42 20 43 5 9 40 34 25 16 10 41 45 7 30 8 36 18 31 24 2 46 22 37 38 6 33 35 11 21 23 3 49

  1 22 47 23 37 40 5 33 35 18 19 6 16 48 12 42 7 41 30 39 4 36 21 26 25 24 29 14 46 11 20 9 43 8 38 2 34 44 31 32 15 17 45 10 13 27 3 28 49

  
  Question: is it possible to find a pandiagonal square of order 7 with 28 irregular lines?
  It is maybe possible. If I have time, I will apply the same method as for symmetrical pandiagonal squares to try to find examples.